An Application in Matrix Theory:Harris Corner Detection
littletree / 2023-12-19
这学期选了一门矩阵论的课,其中有个作业是小组组队科普一些矩阵论的相关应用。我们组选了Harris Corner detection作为报告题目,我负责代码实现部分,花时间整理了下这方面的东西,感觉角点检测还是蛮有意思的,主要是没想到矩阵论在cv处理中还可以这么用。T_T
对于灰度图上某点,如果该点在进行微小移动后灰度变化很大,这意味着该点的亮度或颜色深浅变化显著。这种显著的灰度变化通常发生在图像中的角点corner。
“灰度”是指图像中每个像素点的亮度或颜色深浅。在数字图像处理中,灰度图是一种特殊的图像,其中每个像素仅包含灰度信息,而不包含颜色信息。灰度值通常是从0(纯黑)到255(纯白)的整数,表示不同的亮度级别。在代码中,我们通常将RGB三通道的像素值取平均,最后得到的单通道图像便为灰度图。
注意,上面所说的“微小的移动”是指在某个区域内沿任意方向移动均会引起灰度变化。以下图为例,在1区域想象有个滑动窗口从下往上,移动越过红线,这时也会引起灰度变化,那么是否能判断它就是角点呢?答案是否定的。
因为,滑动窗口在红框1的位置左右移动,并不会引起灰度变化。但这时如果我们考虑2区域这个交点,可以发现无论是上下或者左右移动均会引起灰度的变化,或者是沿2红框的对角线等各个方向均会引起较大的灰度变化,因此我们能够判断交点处为角点。
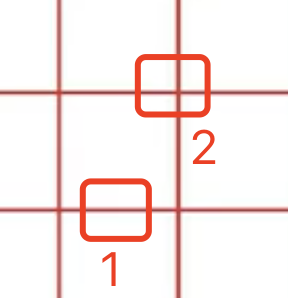
总的来说,角点检测从角点的定义入手,corner的定义为:在该点邻域的各个方向上移动均会引起较大的灰度值变化的点。
粗糙地介绍完了角点检测的原始思想,那如何对其进行数学上的形式化呢?从判断的方法描述中,我提到了可以使用窗口滑动前后灰度值的变化作为判断角点的准则,因此我们可以定义一个表示窗口内灰度值变化的差值函数Error function$E(u,v)$如下
$$
E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2 \tag{1}
$$
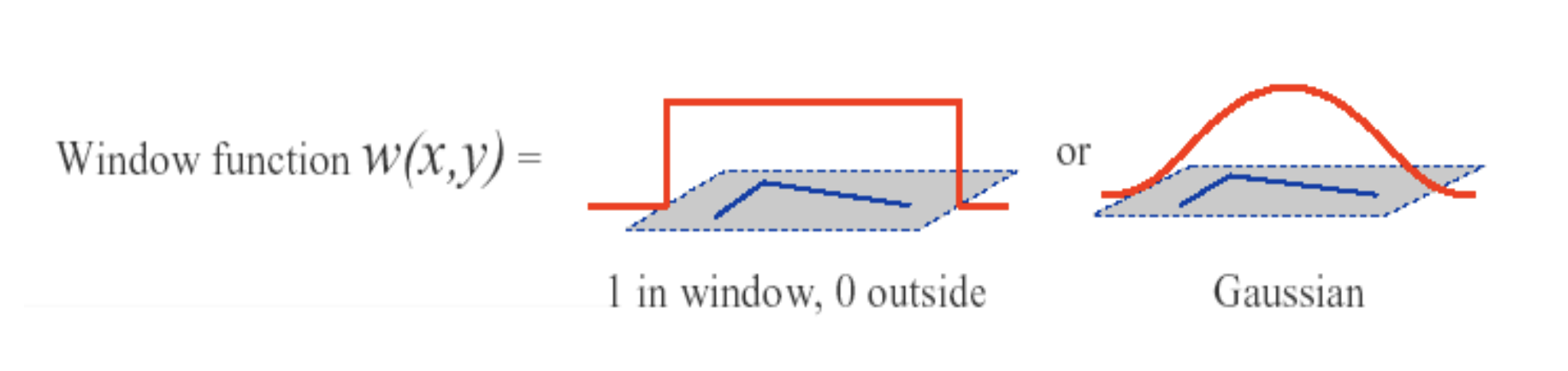
其中$w(x,y)$表示窗口函数,对该点的每个像素点均赋予权值,一般取矩形窗口或者高斯窗口,前者对窗口内的值取1,后者按照高斯分布取值。$I(x+u,y+v)$表示窗口沿u和v平移后的该点的灰度值,$I(x,y)$表示平移前该点的灰度值。求和符号表示对窗口内的所有像素点计算灰度值的变化。
接下来,我们需要对函数$E(u,v)$进行一些化简,首先将$I(x+u,y+v)$在点$(x,y)$处进行一阶Taylor展开,得到下式: $$ E(u,v) \approx \sum_{x,y}w(x,y)[I(x,y)+I_xu+I_yv-I(x,y)]^2 \tag{2} $$ 其中$I_x,I_y$分别表示在点$(x,y)$处的沿$x$和$y$方向的一阶偏导。于是,我们便可以消掉$I(x,y)$,将平方拿进去后得到$I(x,y)$的二次型,那么,很自然地我们会想到把这个二次型写成矩阵的形式,最终的化简结果如下:
$$ E(u,v) \approx [u\quad v]M\begin{bmatrix}u\\v\end{bmatrix} \tag{3} $$
其中矩阵$M$也被称为结构张量structure tensor
$$ M=\sum_{x,y}w(x,y)\begin{bmatrix}I_xI_x&I_xI_y \\ I_xI_y&I_yI_y\end{bmatrix} \tag{4} $$
可以发现差值函数的大小主要取决于$M$的大小,例如,对于开头例子中的1,2区域来说,在滑动窗口移动相同的距离即$u,v$相同的情况下,能检测到区域2中包含角点的原因为是$M$较大。
那么如何来度量$M$对$E$的贡献,从而判断是否存在角点呢?Harris 告诉我们可以使用如下式子来判断某个区域内是否存在corner $$ \begin{aligned}R=\det(M)-k\operatorname{tr}(M)^2.\end{aligned} \tag{5} $$ 由于$\det(M)=\lambda_{1}\lambda_{2}$并且$\operatorname{tr}(M) = \lambda_{1} + \lambda_{2}$,其中$\lambda_{1}\lambda_{2}$分别是矩阵$M$的特征值,于是上式可以进一步展开为: $$ R=\lambda_1\lambda_2-k\left(\lambda_1+\lambda_2\right)^2. \tag{6} $$ 其中$k$是常数,一般取到$[0.04,0.06]$之间
The so-called Harris Corner Detector was introduced by Chris Harris and Mike Stephens in 1988 in the paper “A Combined Corner and Edge Detector”.
因此,我们可以根据结构张量的特征值大小来判断是否包含corner,下图非常形象地说明了这一点:
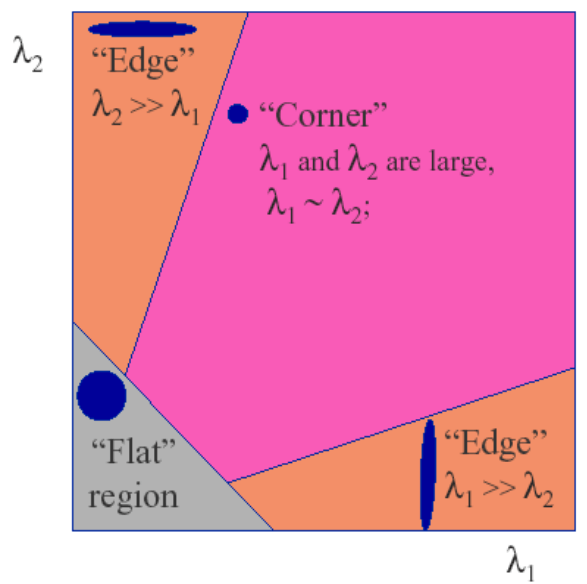
当$\lambda_1\approx\lambda_2$,且都比较大时$R$会比较大,这时可判断存在corner;当$\lambda_1 \gg \lambda_2$,$R < 0$,存在edge;当二者都比较小时,$|R|$较很小,不存在edge或者corner。
其实,根据$\lambda_1\lambda_2$的大小来判断差值函数 $E$ 的大小,从而判断是否存在corner还可以从下面这番推导中也可理解。
由于$M$是一个实对称矩阵,属于正规矩阵,因此$M$酉相似于对角矩阵,且相似变换矩阵$P$为正交矩阵。 我们将$M$相似对角化后带入等式3后,可以得到如下式子
$$ E(u,v)=[u, v]P[\begin{matrix}\lambda_{1}&0\\0&\lambda_{2}\end{matrix}]P^{T}[u,v]^T \tag{7} $$
其中$\lambda_{1},\lambda_{2}$分别为$M$的特征值。由于$P$为正交矩阵,当它与向量相乘,相对于对该向量进行旋转或者反射,因此我们可以把上式写成如下形式:
$$ E(u,v)=[u', v'][\begin{matrix}\lambda_{1}&0\\0&\lambda_{2}\end{matrix}][u',v']^T \\ =\frac{(u^{\prime})^{2}}{\frac{1}{\lambda_{1}}}+\frac{(v^{\prime})^{2}}{\frac{1}{\lambda_{2}}} \tag{8} $$
从几何上,$E(u,v)$可以看作对直角坐标系进行旋转后的一个中心仍在原点的椭圆,如下图。
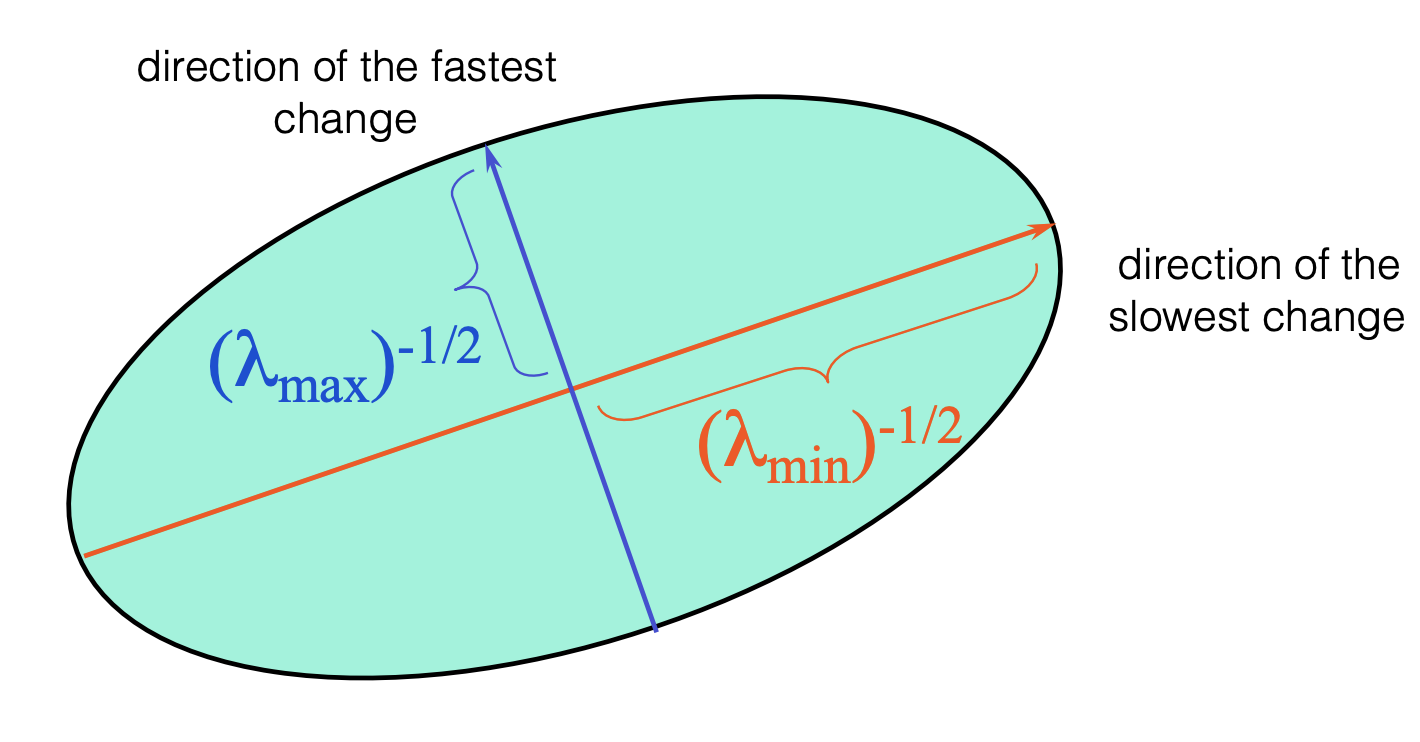
显然,根据式子8,我们便能很清晰地理解如何通过$\lambda_1\lambda_2$的大小来判断是否存在corner了。
实现代码网络上有很多,在此给个pseudo-code做参考
def harris_corner_detection(image, k, window_size, threshold, border):
# 1. Convert to grayscale
gray_image = convert_to_grayscale(image)
# 2. Compute gradients in x and y directions
img_gx = compute_gradient_x(gray_image)
img_gy = compute_gradient_y(gray_image)
# 3. Compute products of gradients
sq_img_gx = img_gx * img_gx
sq_img_gy = img_gy * img_gy
img_gx_gy = img_gx * img_gy
# 4. Apply Gaussian smoothing
sq_img_gx = gaussian_smooth(sq_img_gx, window_size)
sq_img_gy = gaussian_smooth(sq_img_gy, window_size)
img_gx_gy = gaussian_smooth(img_gx_gy, window_size)
# 5. Compute corner response for each pixel
corner_response = compute_corner_response(sq_img_gx, sq_img_gy, img_gx_gy, k)
# 6. Apply thresholding and non-maximum suppression
corners = threshold_and_non_maximum_suppression(corner_response, threshold, window_size)
# 7. Mark corners on the original image
marked_image = mark_corners(image, corners, border)
return marked_image
Reference
- Harris Corner Detection Explained
- Robert Collins, CSE486, Penn State
- 16-385 Computer Vision (Kris Kitani), Carnegie Mellon University
- harris corner detection(角点检测)
- A COMBINED CORNER AND EDGE DETECTOR